by R. Grothmann
The Legendre polynomials are orthogonal on [-1,1] with respect to the weight function 1, i.e., with respect to the Lebesgue measure. They satsify the following recursion formula.
>function L(x,n) &&= block ( if n=0 then 1 else if n=1 then x else ...
((2*n-1)*x*L(x,n-1)-(n-1)*L(x,n-2))/n)
block(if n = 0 then 1 else (if n = 1 then x
(2 n - 1) x L(x, n - 1) - (n - 1) L(x, n - 2)
else ---------------------------------------------))
n
>&L(x,2)
2
3 x - 1
--------
2
Let us check the orthogonality.
>&integrate(L(x,2)*L(x,1),x,-1,1)
0
>&integrate(L(x,2)*L(x,0),x,-1,1)
0
>&integrate(L(x,3)*L(x,2),x,-1,1)
0
The norm of L(x,n) is 2/(2n+1).
>&integrate(L(x,2)*L(x,2),x,-1,1)
2
-
5
They satisfy the following differential equation.
>eq &= -2*x*'diff(y,x)+(1-x^2)*'diff(y,x,2)+n*(n+1)*y=0
2
2 d y dy
(1 - x ) --- - 2 x -- + n (n + 1) y = 0
2 dx
dx
Test for n=3
>& eq | [n=3,y=L(x,3)], & % | nouns | ratsimp
2
5 x (3 x - 1)
2 -------------- - 2 x
2 d 2
(1 - x ) (--- (--------------------))
2 3
dx
2
5 x (3 x - 1)
-------------- - 2 x 2
d 2 5 x (3 x - 1)
- 2 x (-- (--------------------)) + 4 (-------------- - 2 x) = 0
dx 3 2
0 = 0
The main Maxima command ode2 cannot solve this.
>& eq | n=2, &ode2(%,y,x)
2
2 d y dy
(1 - x ) --- - 2 x -- + 6 y = 0
2 dx
dx
false
The two term recursive definition can get ineffective. So we replace it with a loop.
>function L(x,n) &&= block( if n=0 then 1 else block([y:[1,x]], ... for i:2 thru n do y:[y[2],expand(((2*i-1)*x*y[2]-(i-1)*y[1])/i)], y[2]));
Test.
>& L(x,2) | ratsimp
2
3 x - 1
--------
2
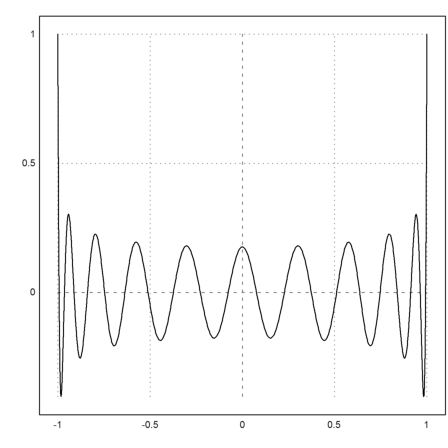
We can now use polynomials of high degree.
>plot2d(& L(x,20) | expand,-1,1):